Selbstinduktion | © C. Wolfseher

Im dargestellten $RL$-Kreis kann man mit einem Umschalter die Spannung $U_0$ abtrennen. Nach dem Ausschalten kann der von der (idealen) Spule induzierte Strom über den Überbrückungswiderstand $R_Ü$ fließen.

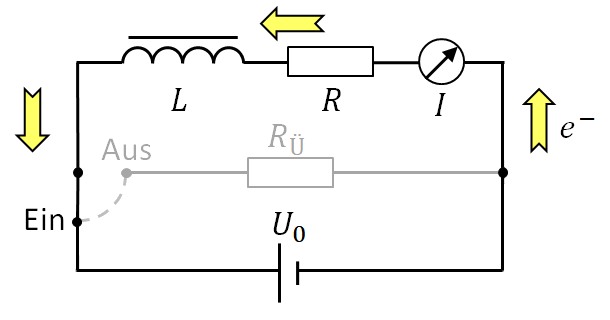
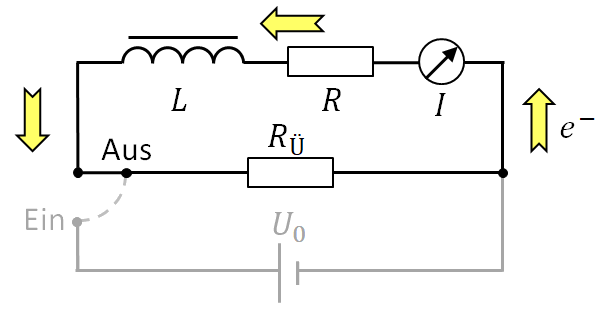
Das folgende Diagramm zeigt den zeitlichen Verlauf des Stroms $I$ und der Induktionsspannung $U_i$ an der Spule beim Ein- und Ausschalten des $RL$-Kreises.

Für den zeitlichen Verlauf der Stromstärke $I(t)$ im (unverzweigten) Stromkreis gilt beim Einschaltvorgang $$I(t)=\frac{U_0+U_i(t)}{R}=\frac{U_0-L\cdot \dot{I}(t)}{R}$$ und damit die Differentialgleichung $$U_0-L\cdot \dot{I}=R\cdot I$$ mit der Lösung

$$I(t) =\frac{{ {{U_0}} }}{R} \cdot \left( {1 - {e^{ - \frac{R}{L} \cdot t}}} \right)$$

Der Strom startet also bei $$I(0)=\frac{{ {{U_0}} }}{R} \cdot \left( {1 - {e^{ - \frac{R}{L} \cdot 0}}} \right)=0$$ und nähert sich asymptotisch dem (ohne Selbstinduktion zu erwartenden) stationären Endstrom: $$\lim\limits_{t\to\infty}\left[\frac{{ {{U_0}} }}{R} \cdot \left( {1 - {e^{ - \frac{R}{L} \cdot t}}} \right)\right]=\frac{{ {{U_0}} }}{R}$$

Mit Kenntnis von $I(t)$ erhält man aus $U_i=-L\cdot \dot{I}$ den zeitlichen Verlauf der an der Spule induzierten Spannung:

$${U_i}(t) = -{{U_0}} \cdot {e^{ - \frac{R}{L} \cdot t}}$$

Im ersten Moment kompensiert die Induktionsspannung $U_i$ die angelegte Spannung $U_0$ $$U_i(0)=-U_0 \cdot e^{ - \frac{R}{L} \cdot 0}=-U_0$$ und versiegt dann allmählich: $$\lim\limits_{t\to\infty}\left( -{{U_0}} \cdot {e^{ - \frac{R}{L} \cdot t}}\right)=0$$

Nach dem Umlegen des Schalters auf die Stellung Aus fungiert im (unverzweigten) Kreis mit dem Gesamtwiderstand $R+R_Ü$ allein die Spule mit der Induktionsspannung $U_i$ als Stromquelle. Folglich gilt für den zeitlichen Verlauf der Stromstärke $I(t)$ beim Ausschaltvorgang $$I(t)=\frac{U_i(t)}{R+R_Ü}=\frac{-L\cdot \dot{I}(t)}{R+R_Ü}$$ und damit die Differentialgleichung $$(R+R_Ü)\cdot I+L \cdot \dot{I}=0$$ mit der Lösung

$$I(t) = I_0 \cdot e^{ - \frac{R+R_Ü}{L} \cdot t}$$

Der Strom fällt also exponentiell von $$I(0)=I_0 \cdot e^{ - \frac{R+R_Ü}{L} \cdot 0} =I_0$$ (wobei $I_0=\frac{U_0}{R}$, falls die Spule vorher lange genug eingeschaltet war) auf $$\lim\limits_{t\to\infty}\left(I_0 \cdot e^{ - \frac{R+R_Ü}{L} \cdot t}\right)=0$$ ab.

Mit Kenntnis von $I(t)$ erhält man aus $U_i=-L\cdot \dot{I}$ den zeitlichen Verlauf der an der Spule induzierten Spannung:

$${U_i}(t) = (R+R_Ü) \cdot I_0 \cdot e^{ - \frac{R+R_Ü}{L} \cdot t}$$

Beim Ausschalten können Spitzen der Induktionsspannung $U_i$ $$U_i(0)=(R+R_Ü) \cdot I_0 \cdot e^{ - \frac{R+R_Ü}{L} \cdot 0}=(R+R_Ü) \cdot I_0$$ auftreten, die weit über $U_0$ liegen. Falls $I_0= \frac{U_0}{R}$, gilt: $$U_i(0)= U_0+ \frac{R_Ü}{R}\cdot U_0 \ge U_0$$ Doch auch das Aufbäumen von $U_i$ nimmt ein Ende: $$\lim\limits_{t\to\infty}\left[ (R+R_Ü) \cdot I_0 \cdot e^{ - \frac{R+R_Ü}{L} \cdot t}\right]=0$$

Beim Einschaltvorgang ändert sich der magnetische Fluss $\Phi$ von 0 bis zum Maximalwert $\Phi_{\text{max}}$. Beim Ausschaltvorgang nimmt $\Phi$ von $\Phi_{\text{max}}$ bis auf 0 ab.

Nach dem Induktionsgesetz in integraler Form

$$\int\limits_{t_1}^{t_2}U_i(t)\ \mathrm{d}t=-N\left[\Phi(t_2)-\Phi(t_1)\right]$$

sind damit die Integralwerte für den Ein- und Ausschaltvorgang bis auf das Vorzeichen gleich:

$$\int\limits_{t_{\text{Ein}}}^{t_{\text{Aus}}}U_i(t)\ \mathrm{d}t=-\int\limits_{t_{\text{Aus}}}^{\infty}U_i(t)\ \mathrm{d}t$$

Im obigen Diagramm werden diese Integralwerte durch schattierte Flächen veranschaulicht.

Selbstinduktion | Ein- und Ausschalten von RL-Kreisen