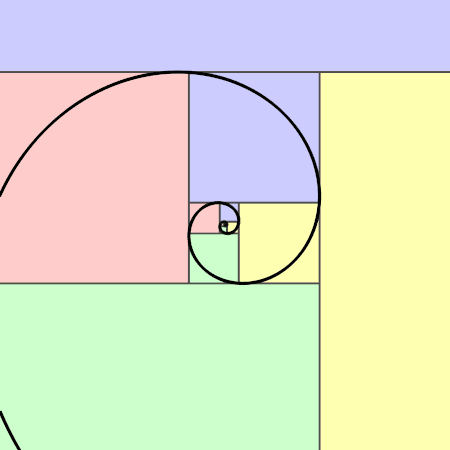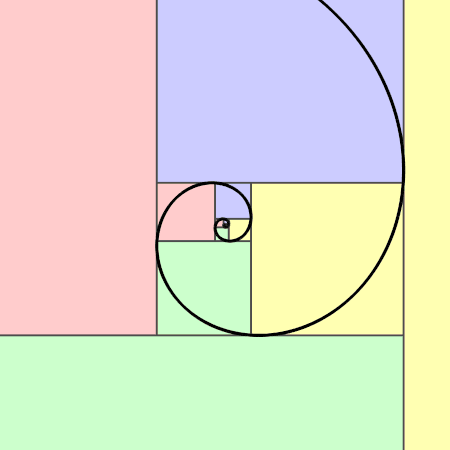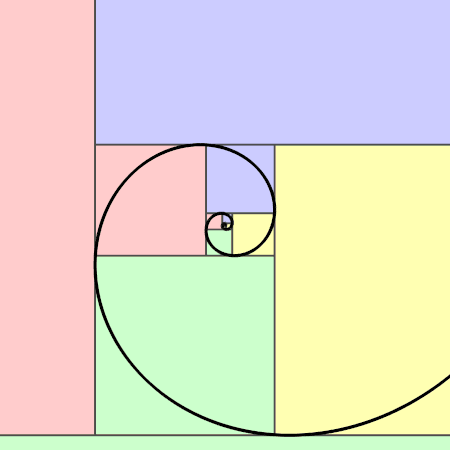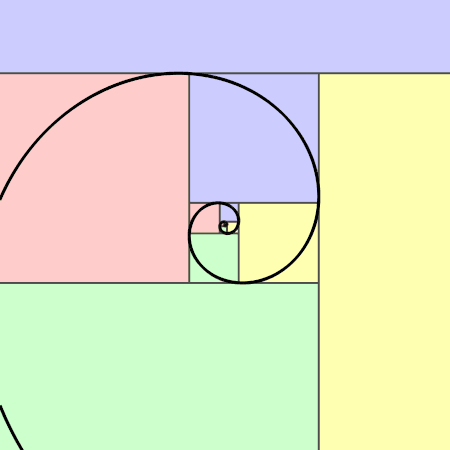
 Die im obigen Bild eingezeichneten Diagonalen — deren Längenverhältnis übrigens \(\varphi\) ist —
verlaufen auch durch alle entsprechenden Rechtecke diagonal.
Die im obigen Bild eingezeichneten Diagonalen — deren Längenverhältnis übrigens \(\varphi\) ist —
verlaufen auch durch alle entsprechenden Rechtecke diagonal.
Die soeben gezeigte Konstruktion zur äußeren Teilung, lässt uns
ein Quadrat zu einem Goldenen Rechteck
ergänzen,
bei dem die
Länge \(l = \varphi \, \cdot\) Breite \(b\)
hier normiert: \(b=1\) und \(l=\varphi\)
ist.
Das konstruierte Goldene Rechteck besteht aus einem Quadrat und einem — weiteren, kleineren Goldenen Rechteck mit der Länge \(1\) und Breite \(\varphi -1\overset{(3)}=\frac{1}{\varphi}\). Wir können folglich Goldene Rechtecke Nur Goldene Rechtecke lassen sich in ein Quadrat und ein ähnliches Rechteck zerlegen. wiederholt in Quadrate und Goldene Rechtecke zerlegen.
 Die im obigen Bild eingezeichneten Diagonalen — deren Längenverhältnis übrigens \(\varphi\) ist —
verlaufen auch durch alle entsprechenden Rechtecke diagonal.
Die im obigen Bild eingezeichneten Diagonalen — deren Längenverhältnis übrigens \(\varphi\) ist —
verlaufen auch durch alle entsprechenden Rechtecke diagonal.
Der Schnittpunkt der Diagonalen wird zuweilen Das Auge Gottes
genannt.
Es ist der Ursprung einer
Goldenen Spirale
logarithmische Spirale $$r(\alpha)={\varphi}^{\frac{2}{\pi}\alpha}$$
, deren Radius sich bei jeder Vierteldrehung um das \(\varphi\)-fache ändert. Man kann die Spirale durch Viertelkreise approximieren.
erstellt von C. Wolfseher