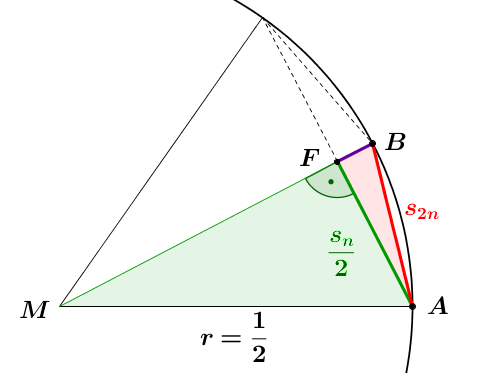
| Im rechtwinkligen Dreieck \(FAB\) liefert der Satz des Pythagoras: $$\left(\color{red}{s_{2n}}\right)^2=\left(\color{green}{\frac{s_n}{2}}\right)^2+\color{purple}{\overline{FB}}^2 \tag{1}$$ Außerdem gilt: $$\color{purple}{\overline{FB}}=\frac{1}{2}-\overline{MF} \tag{2}$$ |

|
Also gilt: $$\bbox[#f0ffff,1pt]{s_{2n}}=\sqrt{\frac{1}{2}-\frac{1}{2}\sqrt{1-\bbox[#fff0ff,1pt]{s_n}^2}}$$
\begin{align} \left(s_{2n}\right)^2 &=\left(\frac{s_n}{2}\right)^2 + \left(\frac{1}{2}-\sqrt{\left(\frac{1}{2}\right)^2-\left(\frac{s_n}{2}\right)^2}\right)^2\\ &=\cssId{Step1}{\left(\frac{s_n}{2}\right)^2 + \left(\frac{1}{2}-\frac{1}{2}\sqrt{1-{s_n}^2}\right)^2}\\ &=\cssId{Step2}{\left(\frac{s_n}{2}\right)^2 + \left(\frac{1}{4}-2\cdot\frac{1}{2}\cdot\frac{1}{2}\sqrt{1-{s_n}^2}+\frac{1}{4}\left({1-{s_n}^2}\right)\right)}\\ &=\cssId{Step3}{\frac{1}{4}{s_n}^2 + \frac{1}{4} - \frac{1}{2}\sqrt{1-{s_n}^2}+\frac{1}{4}-\frac{1}{4}{s_n}^2}\\ &=\cssId{Step4}{\frac{1}{2}-\frac{1}{2}\sqrt{1-{s_n}^2};}\\ \end{align}
Da für den Umfang \(u_n=n \cdot s_n\) und damit \(s_n=\frac{u_n}{n}\) gilt, folgt:
\begin{align} u_{2n} &=2n \cdot \bbox[#f0ffff,1pt]{s_{2n}}\\ &=2n \cdot\sqrt{\frac{1}{2}-\frac{1}{2}\sqrt{1-\left(\bbox[#fff0ff,1pt]{\frac{u_n}{n}}\right)^2}}\\ &=n \cdot\sqrt{2-2\sqrt{1-\left(\frac{u_n}{n}\right)^2}}\\ \end{align}
Archimedes rechnete (ohne Taschenrechner) bis zum 96-Eck. Für die Wurzeln verwendete er rationale Näherungswerte und kam somit zum Ergebnis $$3\frac{10}{71}\approx 3,1408450704\lt\pi$$
Um noch näher an \(\pi\) 'ranzukommen, müssen wir – oder besser: der Computer – die Eckenzahl noch öfter verdoppeln …