$$n \cdot \sqrt{2-2\sqrt{1-\left(\frac{u_n}{n}\right)^2}} \cdot \sqrt{2+2\sqrt{1-\left(\frac{u_n}{n}\right)^2}}$$ \begin{align} &=\cssId{Step1}{n \cdot \sqrt{\left(2-2\sqrt{1-\left(\frac{u_n}{n}\right)^2}\right)\cdot \left(2+2\sqrt{1-\left(\frac{u_n}{n}\right)^2}\right)}}\\ &=\cssId{Step2}{n \cdot \sqrt{4-4\left(1-\left(\frac{u_n}{n}\right)^2\right)}}\\ &=\cssId{Step3}{2n \cdot \sqrt{1-1+\left(\frac{u_n}{n}\right)^2}}\\ &=\cssId{Step4}{2n \cdot \frac{u_n}{n}}\\ &=\cssId{Step5}{2u_n;}\\ \end{align}
Der Lohn unserer Mühen ist eine auch gegen computerbedingte Rundungsfehler gewappnete
|
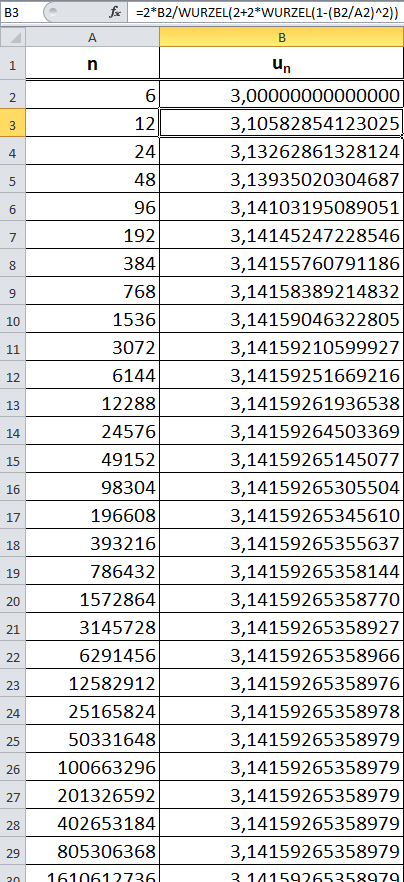
Wir verwenden nun unsere verbesserte Iterationsformel: \(u_n\) sind wieder die Umfänge der einbeschriebenen, regulären \(n\)-Ecke eines Kreises mit dem Radius \(r=0,5\). Mit wachsender Anzahl an Iterationen gibt \(\pi\) immer mehr Dezimalen preis. Aber genau genommen sind wir noch nicht ganz fertig... |
|