Integralfunktion | ohne \(\int\)

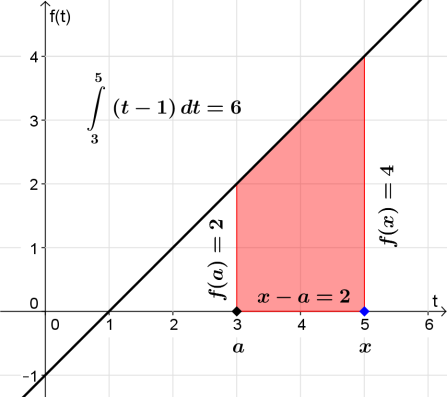
Für \(1 < a < x\) beispielsweise ist \(I_a(x)\) die Maßzahl der Fläche eines Trapezes mit den Grundseiten der Länge \(f(a)\) und \(f(x)\) und der Höhe der Länge \(x-a\).

Drücke die Trapezfläche durch \(x\) und \(a\) aus:

\begin{align} A_{Trapez} &=\cssId{Step1}{\frac{1}{2}\cdot\left(\mbox{1. Grundseite + 2. Grundseite}\right)\cdot\mbox{Höhe}}\\ &=\cssId{Step2}{\frac{1}{2}\cdot\left(f(x)+f(a)\right)\cdot(x-a)}\\ &=\cssId{Step3}{\frac{1}{2}\cdot\left((x-1)+(a-1)\right)\cdot(x-a)}\\ &=\cssId{Step4}{\frac{1}{2}\cdot\left(x+a-2\right)\cdot(x-a)}\\ &=\cssId{Step5}{\frac{1}{2}\cdot\left(x^2-ax+ax-a^2-2x+2a\right)}\\ &=\cssId{Step6}{\left(\frac{1}{2}x^2-x\right)-\left(\frac{1}{2}a^2-a\right);}\\ \end{align}

• Schreibe \(I_3(x)\) ohne \(\int\) ! $$I_3(x)=\int\limits_3^x{(t-1)dt}=\frac{1}{2}x^2-x-\left(\frac{1}{2}3^2-3\right)=\frac{1}{2}x^2-x-1,5$$
• Für welche \(a\) gilt \(I_a(x)=\frac{1}{2}x^2-x\) ? $$I_a(x)=\frac{1}{2}x^2-x \Leftrightarrow \frac{1}{2}a^2-a=0 \Leftrightarrow a=0 \lor a=2$$
• Welcher erstaunliche Zusammenhang besteht zwischen der Integrandenfunktion \(f(t)=t-1\) und der Integralfunktion \(I_a(x)=\int\limits_a^x{f(t)dt}\) ? Die Integralfunktion ist eine Stammfunktion der Integrandenfunktion: \(I'_a(x)=f(x)\)

  Zufall?

«    •    »

erstellt von C. Wolfseher